Boosted Trees 介绍

XGBoost 代表“极限梯度提升”，其中“梯度提升”一词源自 Friedman 的论文《Greedy Function Approximation: A Gradient Boosting Machine》。

梯度提升树这个术语已经存在一段时间了，关于这个主题有很多资料。本教程将使用监督学习的元素，以一种自洽且有原则的方式解释提升树。我们认为这种解释更清晰、更正式，并能更好地激发 XGBoost 中使用的模型公式。

监督学习的要素

XGBoost 用于监督学习问题，我们使用训练数据（具有多个特征）\(x_i\) 来预测目标变量\(y_i\)。在我们专门学习树之前，让我们先回顾一下监督学习的基本要素。

模型和参数

监督学习中的模型通常指从输入\(x_i\)生成预测\(y_i\)的数学结构。一个常见的例子是线性模型，其中预测表示为\(\hat{y}_i = \sum_j \theta_j x_{ij}\)，是加权输入特征的线性组合。预测值可以有不同的解释，取决于任务，即回归或分类。例如，它可以进行逻辑转换以获得逻辑回归中正类的概率，也可以用作排名分数，当我们想要对输出进行排名时。

参数是我们从数据中学习的未确定部分。在线性回归问题中，参数是系数\(\theta\)。通常我们将用\(\theta\)表示参数（一个模型中有很多参数，我们这里的定义比较粗略）。

目标函数：训练损失 + 正则化

通过谨慎选择\(y_i\)，我们可以表达各种任务，例如回归、分类和排名。训练模型的任务归结为找到最能拟合训练数据\(x_i\)和标签\(y_i\)的最佳参数\(\theta\)。为了训练模型，我们需要定义目标函数来衡量模型拟合训练数据的程度。

目标函数的一个显著特点是它们由两部分组成：训练损失和正则化项

\[\text{obj}(\theta) = L(\theta) + \Omega(\theta)\]

其中\(L\)是训练损失函数，\(\Omega\)是正则化项。训练损失衡量我们的模型对训练数据的预测性。一种常见的\(L\)选择是均方误差，其定义为

\[L(\theta) = \sum_i (y_i-\hat{y}_i)^2\]

另一个常用的损失函数是逻辑损失，用于逻辑回归

\[L(\theta) = \sum_i[ y_i\ln (1+e^{-\hat{y}_i}) + (1-y_i)\ln (1+e^{\hat{y}_i})]\]

正则化项是人们通常忘记添加的部分。正则化项控制模型的复杂度，这有助于我们避免过拟合。这听起来有点抽象，所以让我们看下面图片中的问题。你被要求根据图片左上角给出的输入数据点，视觉上拟合一个阶跃函数。你认为三者中哪个解决方案最合适？

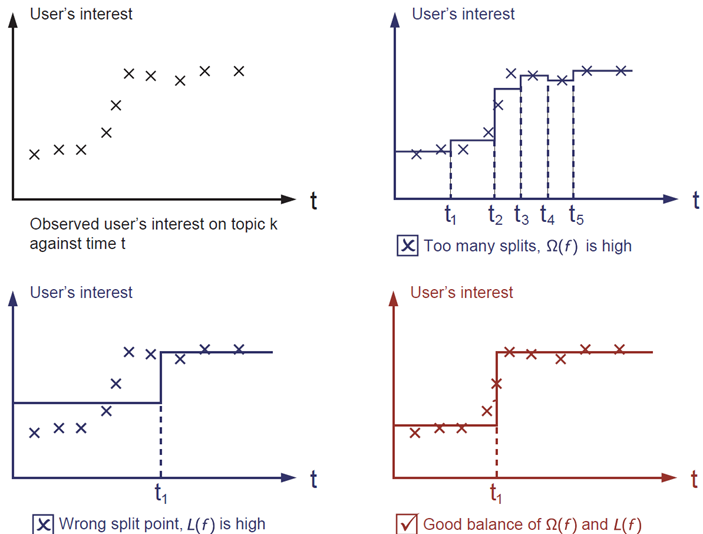
正确答案以红色标记。请考虑这在视觉上对你来说是否是一个合理的拟合。一般原则是我们希望模型既简单又具有预测性。两者之间的权衡在机器学习中也被称为偏差-方差权衡。

为什么要引入一般原则？

上面介绍的元素构成了监督学习的基本元素，它们是机器学习工具包的自然构建块。例如，你应该能够描述梯度提升树和随机森林之间的区别和共同点。以形式化的方式理解这个过程也有助于我们理解我们正在学习的目标以及剪枝和平滑等启发式方法背后的原因。

决策树集成

现在我们已经介绍了监督学习的要素，让我们开始学习真正的树。首先，让我们先了解 XGBoost 的模型选择：决策树集成。树集成模型由一组分类和回归树（CART）组成。这是一个简单的 CART 示例，它分类某人是否会喜欢一个假设的电脑游戏 X。

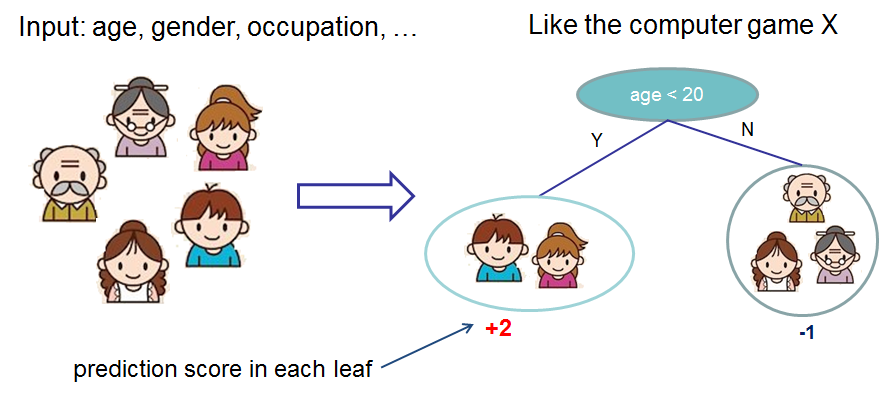
我们将一个家庭的成员分类到不同的叶子中，并给他们分配相应叶子的分数。CART 与决策树有点不同，决策树的叶子只包含决策值。在 CART 中，每个叶子都关联一个真实分数，这为我们提供了超出分类范围的更丰富的解释。这也允许了一种有原则的统一优化方法，我们将在本教程的后面部分看到。

通常，单个树在实践中不够强大。实际使用的是集成模型，它将多棵树的预测相加。

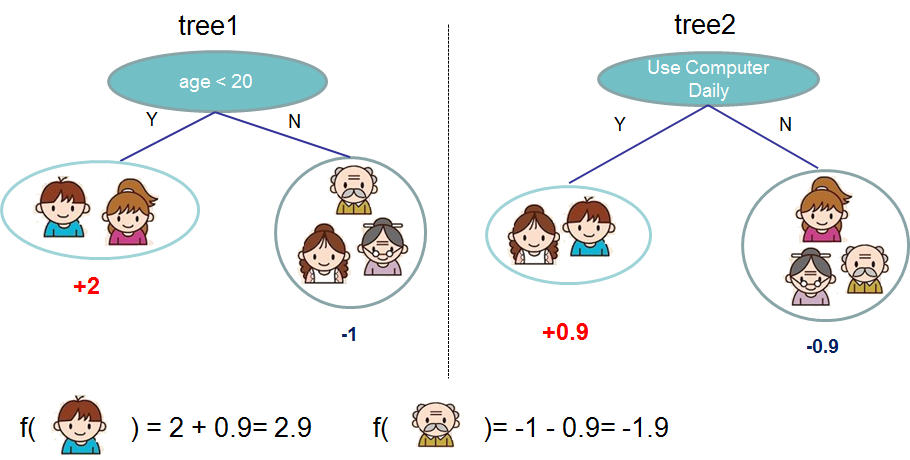
这是两棵树的树集成示例。每个单独的树的预测分数相加得到最终分数。如果你看这个例子，一个重要的事实是这两棵树试图相互补充。在数学上，我们可以将我们的模型写成以下形式

\[\hat{y}_i = \sum_{k=1}^K f_k(x_i), f_k \in \mathcal{F}\]

其中\(K\)是树的数量，\(f_k\)是函数空间\(\mathcal{F}\)中的一个函数，\(\mathcal{F}\)是所有可能的 CART 的集合。要优化的目标函数由下式给出

\[\text{obj}(\theta) = \sum_i^n l(y_i, \hat{y}_i) + \sum_{k=1}^K \omega(f_k)\]

其中\(\omega(f_k)\)是树\(f_k\)的复杂度，稍后将详细定义。

现在有一个难题：随机森林中使用的模型是什么？树集成！所以随机森林和提升树实际上是相同的模型；区别在于我们如何训练它们。这意味着，如果你为树集成编写预测服务，你只需要编写一个，它应该适用于随机森林和梯度提升树。（有关实际示例，请参阅Treelite。）这是监督学习要素为何如此出色的一个例子。

树提升

现在我们已经介绍了模型，让我们转向训练：我们应该如何学习树？答案是，对于所有监督学习模型来说都是如此：定义一个目标函数并优化它！

令以下为目标函数（记住它总是需要包含训练损失和正则化）

\[\text{obj} = \sum_{i=1}^n l(y_i, \hat{y}_i^{(t)}) + \sum_{k=1}^t\omega(f_k)\]

其中\(t\)是我们集成中的树的数量。（每个训练步骤将添加一棵新树，因此在步骤\(t\)时，集成包含\(K=t\)棵树）。

加性训练

我们想问的第一个问题是：树的参数是什么？你会发现我们需要学习的是那些函数\(f_k\)，每个函数都包含树的结构和叶子分数。学习树结构比传统的优化问题要困难得多，在传统的优化问题中你可以简单地取梯度。一次性学习所有树是不可行的。相反，我们使用一种加性策略：固定我们已经学到的东西，每次添加一棵新树。我们将步骤\(t\)的预测值写为\(\hat{y}_i^{(t)}\)。那么我们有

\[\begin{split}\hat{y}_i^{(0)} &= 0\\ \hat{y}_i^{(1)} &= f_1(x_i) = \hat{y}_i^{(0)} + f_1(x_i)\\ \hat{y}_i^{(2)} &= f_1(x_i) + f_2(x_i)= \hat{y}_i^{(1)} + f_2(x_i)\\ &\dots\\ \hat{y}_i^{(t)} &= \sum_{k=1}^t f_k(x_i)= \hat{y}_i^{(t-1)} + f_t(x_i)\end{split}\]

剩下的问题是：我们每一步想要哪棵树？一个自然的想法是添加优化我们目标的那棵树。

\[\begin{split}\text{obj}^{(t)} & = \sum_{i=1}^n l(y_i, \hat{y}_i^{(t)}) + \sum_{k=1}^t\omega(f_k) \\ & = \sum_{i=1}^n l(y_i, \hat{y}_i^{(t-1)} + f_t(x_i)) + \omega(f_t) + \mathrm{constant}\end{split}\]

如果我们考虑使用均方误差 (MSE) 作为损失函数，目标变为

\[\begin{split}\text{obj}^{(t)} & = \sum_{i=1}^n (y_i - (\hat{y}_i^{(t-1)} + f_t(x_i)))^2 + \sum_{k=1}^t\omega(f_k) \\ & = \sum_{i=1}^n [2(\hat{y}_i^{(t-1)} - y_i)f_t(x_i) + f_t(x_i)^2] + \omega(f_t) + \mathrm{constant}\end{split}\]

MSE 的形式很友好，带有一阶项（通常称为残差）和二次项。对于其他感兴趣的损失（例如，逻辑损失），要获得如此好的形式就不那么容易了。所以在一般情况下，我们对损失函数进行二阶泰勒展开

\[\text{obj}^{(t)} = \sum_{i=1}^n [l(y_i, \hat{y}_i^{(t-1)}) + g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \omega(f_t) + \mathrm{constant}\]

其中\(g_i\)和\(h_i\)定义为

\[\begin{split}g_i &= \partial_{\hat{y}_i^{(t-1)}} l(y_i, \hat{y}_i^{(t-1)})\\ h_i &= \partial_{\hat{y}_i^{(t-1)}}^2 l(y_i, \hat{y}_i^{(t-1)})\end{split}\]

在移除所有常数后，步骤\(t\)的具体目标变为

\[\sum_{i=1}^n [g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \omega(f_t)\]

这成为我们新树的优化目标。这个定义的一个重要优点是目标函数的值只取决于\(g_i\)和\(h_i\)。这就是 XGBoost 如何支持自定义损失函数。我们可以使用完全相同的求解器来优化每个损失函数，包括逻辑回归和成对排名，该求解器以\(g_i\)和\(h_i\)作为输入！

模型复杂度

我们已经介绍了训练步骤，但是等等，还有一件重要的事情，那就是正则化项！我们需要定义树的复杂度\(\omega(f)\)。为此，我们首先将树\(f(x)\)的定义细化为

\[f_t(x) = w_{q(x)}, w \in R^T, q:R^d\rightarrow \{1,2,\cdots,T\} .\]

这里\(w\)是叶子上的分数向量，\(q\)是一个将每个数据点分配到相应叶子的函数，\(T\)是叶子的数量。在 XGBoost 中，我们将复杂度定义为

\[\omega(f) = \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T w_j^2\]

当然，定义复杂度的方法不止一种，但这种方法在实践中效果很好。正则化是大多数树包处理不够仔细或直接忽略的一部分。这是因为传统的树学习方法只强调提高纯度，而复杂度控制则留给了启发式方法。通过正式定义它，我们可以更好地了解我们正在学习什么，并获得在实际中表现良好的模型。

结构得分

这是推导的神奇之处。在重新构造树模型之后，我们可以将包含第\(t\)棵树的目标值写为

\[\begin{split}\text{obj}^{(t)} &\approx \sum_{i=1}^n [g_i w_{q(x_i)} + \frac{1}{2} h_i w_{q(x_i)}^2] + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T w_j^2\\ &= \sum^T_{j=1} [(\sum_{i\in I_j} g_i) w_j + \frac{1}{2} (\sum_{i\in I_j} h_i + \lambda) w_j^2 ] + \gamma T\end{split}\]

其中\(I_j = \{i|q(x_i)=j\}\)是分配到第\(j\)个叶子上的数据点的索引集合。请注意，在第二行中我们改变了求和的索引，因为同一叶子上的所有数据点获得相同的分数。我们可以通过定义\(G_j = \sum_{i\in I_j} g_i\)和\(H_j = \sum_{i\in I_j} h_i\)来进一步压缩表达式

\[\text{obj}^{(t)} = \sum^T_{j=1} [G_jw_j + \frac{1}{2} (H_j+\lambda) w_j^2] +\gamma T\]

在这个方程中，\(w_j\)是相互独立的，形式\(G_jw_j+\frac{1}{2}(H_j+\lambda)w_j^2\)是二次的，对于给定的结构\(q(x)\)，最佳\(w_j\)以及我们可以获得的最佳目标减少是

\[\begin{split}w_j^\ast &= -\frac{G_j}{H_j+\lambda}\\ \text{obj}^\ast &= -\frac{1}{2} \sum_{j=1}^T \frac{G_j^2}{H_j+\lambda} + \gamma T\end{split}\]

最后一个方程衡量树结构\(q(x)\)的好坏程度。

如果这一切听起来有点复杂，让我们看一看这张图，看看分数是如何计算的。基本上，对于给定的树结构，我们将统计量\(g_i\)和\(h_i\)推送到它们所属的叶子，将统计量加在一起，然后使用公式计算树的好坏。这个分数就像决策树中的纯度度量一样，但它也考虑了模型的复杂度。

学习树结构

现在我们有了一种衡量树好坏的方法，理想情况下，我们会枚举所有可能的树并选择最好的。在实践中这是不可行的，所以我们将尝试一次优化树的一个级别。具体来说，我们尝试将一个叶子分成两个叶子，它获得的分数是

\[Gain = \frac{1}{2} \left[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}\right] - \gamma\]

这个公式可以分解为：1) 新左叶子的得分 2) 新右叶子的得分 3) 原始叶子的得分 4) 附加叶子的正则化。我们可以在这里看到一个重要的事实：如果增益小于\(\gamma\)，我们最好不要添加该分支。这正是基于树的模型中的剪枝技术！通过使用监督学习的原则，我们自然可以找出这些技术有效的原因 :)

对于实值数据，我们通常希望寻找最佳分割。为了有效地做到这一点，我们将所有实例按排序顺序放置，如下图所示。

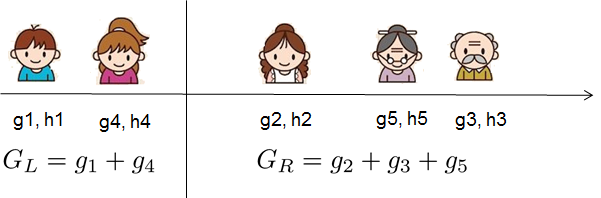
从左到右扫描足以计算所有可能分割方案的结构得分，我们可以有效地找到最佳分割。

注意

加性树学习的局限性

由于枚举所有可能的树结构是不可行的，我们一次添加一个分割。这种方法在大多数情况下效果很好，但由于这种方法，存在一些失败的边缘情况。对于这些边缘情况，训练会导致模型退化，因为我们一次只考虑一个特征维度。有关示例，请参阅梯度提升能学习简单的算术吗？。

关于 XGBoost 的最后几句话

现在你已经了解了什么是提升树，你可能会问，XGBoost 的介绍在哪里？XGBoost 正是本教程中介绍的正式原则所激发的工具！更重要的是，它在系统优化和机器学习原则方面都进行了深入考虑。该库的目标是突破机器计算能力的极限，提供一个可扩展、可移植和准确的库。务必尝试一下，最重要的是，将你的智慧（代码、示例、教程）贡献给社区！